As MDNs não apenas prevêem o valor esperado de um alvo, mas também a distribuição de probabilidade subjacente.
Este post do blog se concentrará em como implementar esse modelo usando o Tensorflow, desde o início, incluindo explicações, diagramas e um notebook Jupyter com todo o código-fonte .
O que são MDNs e por que são úteis?
Os dados da vida real são barulhentos. Embora bastante irritante, esse ruído é significativo, pois oferece uma perspectiva mais ampla das origens dos dados. O valor alvo pode ter diferentes níveis de ruído, dependendo da entrada, e isso pode ter um grande impacto na nossa compreensão dos dados.
Isso é melhor explicado com um exemplo. Assuma a seguinte função quadrática:
Dado x como entrada, temos uma saída determinística f (x) . Agora, vamos transformar essa função em uma função mais interessante (e realista): adicionaremos algum ruído normalmente distribuído a f (x) . Esse ruído aumentará à medida que x aumentar. Vamos chamar a nova função g (x) , que formalmente é igual a g (x) = f (x) + ? (x) , onde ? (x) é uma variável aleatória normal.
Vamos amostrar g (x) para diferentes valores de x :

A linha roxa representa a função silenciosa f (x) , e podemos ver facilmente o aumento do ruído adicionado. Vamos inspecionar os casos onde x = 1 e x = 5 . Para esses dois valores, f (x) = 4 e , portanto, 4 é um valor razoável que g (x) pode assumir. 4.5 também é uma previsão razoável para g (x)? A resposta é claramente não. Enquanto 4.5 parece ser um valor razoável para x = 5 , não podemos aceitá-lo como um valor válido para g (x) quando x = 1 . Se nosso modelo simplesmente aprender a prever y '(x) = f (x) , essas informações valiosas serão perdidas. O que realmente precisamos aqui é de um modelo capaz de prever y '(x) = g (x). E é exatamente isso que um MDN faz.
O conceito de MDN foi inventado por Christopher Bishop em 1994. Seu artigo original explica muito bem o conceito, mas remonta à era pré-histórica em que as redes neurais não eram tão comuns como são hoje. Portanto, falta a parte prática de como realmente implementar uma. E é exatamente isso que vamos fazer agora.
Vamos começar
Vamos começar com uma rede neural simples que apenas aprende f (x) a partir do conjunto de dados barulhento. Usaremos 3 camadas densas ocultas, cada uma com 12 nós, mais ou menos assim:

Usaremos o erro quadrático médio como a função de perda. Vamos codificar isso no Tensorflow:
1 2 3 4 5 | x = tf.placeholder(name='x',shape=(None,1),dtype=tf.float32) layer = x for _ in range(3): layer = tf.layers.dense(inputs=layer, units=12, activation=tf.nn.tanh) output = tf.layers.dense(inputs=layer, units=1) |
Após o treinamento, a saída fica assim:

Vemos a rede aprendida com sucesso f (x) . Agora, tudo o que falta é uma estimativa do ruído. Vamos modificar a rede para obter essa informação adicional.
Going MDN
Continuaremos usando a mesma rede que acabamos de projetar, mas alteraremos duas coisas:
- A camada de saída terá dois nós em vez de um, e os nomearemos mu e sigma
- Usaremos uma função de perda diferente
Agora nossa rede fica assim:

Vamos codificá-lo:
1 2 3 4 5 6 | x = tf.placeholder(name='x',shape=(None,1),dtype=tf.float32) layer = x for _ in range(3): layer = tf.layers.dense(inputs=layer, units=12, activation=tf.nn.tanh) mu = tf.layers.dense(inputs=layer, units=1) sigma = tf.layers.dense(inputs=layer, units=1,activation=lambda x: tf.nn.elu(x) + 1) |
Vamos dar um segundo para entender a função de ativação do sigma - lembre-se de que, por definição, o desvio padrão de qualquer distribuição é um número não negativo. A Unidade Linear Exponencial (ELU), definida como:
produz -1 como seu valor mais baixo e, portanto, ELU + 1 sempre será não negativo. Tem que ser ELU? Não, qualquer função que sempre produz uma saída não negativa fará - por exemplo, o valor absoluto de sigma. ELU simplesmente parece estar fazendo um trabalho melhor.
Em seguida, precisamos ajustar nossa função de perda. Vamos tentar entender exatamente o que estamos procurando agora. Nossa nova camada de saída nos fornece os parâmetros de uma distribuição normal. Essa distribuição deve ser capaz de descrever os dados gerados pela amostragem g (x) . Como podemos medir isso? Podemos, por exemplo, criar uma distribuição normal a partir da saída e maximizar a probabilidade de amostrar nossos valores-alvo a partir dela. Matematicamente, gostaríamos de maximizar os valores da função de densidade de probabilidade (PDF) da distribuição normal para todo o conjunto de dados. Equivalentemente, podemos minimizar o logaritmo negativo do PDF:

Podemos ver que a função de perda é diferenciável em relação a ? e ?. Você ficará surpreso com a facilidade de codificar:
1 2 | dist = tf.distributions.Normal(loc=mu, scale=sigma) loss = tf.reduce_mean(-dist.log_prob(y)) |
E é sobre isso. Depois de treinar o modelo, podemos ver que ele realmente captou g (x) :
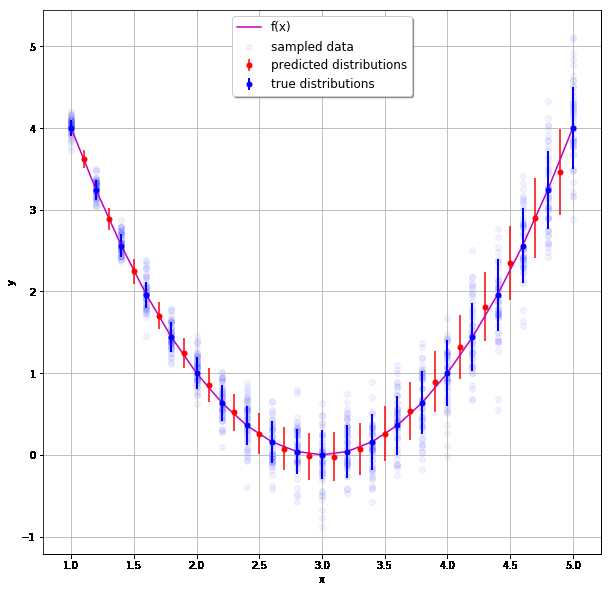
No gráfico acima, as linhas e pontos azuis representam o desvio padrão real e a média usados para gerar os dados, enquanto as linhas e pontos vermelhos representam os mesmos valores previstos pela rede para valores x não vistos . Grande sucesso!
Próximos passos
Vimos como prever uma distribuição normal simples - mas nem é preciso dizer que os MDNs podem ser muito mais gerais - podemos prever distribuições completamente diferentes, ou mesmo uma combinação de várias distribuições diferentes. Tudo o que você precisa fazer é ter um nó de saída para cada parâmetro das variáveis da distribuição e validar se o PDF da distribuição é diferenciável.
Só posso encorajá-lo a tentar prever distribuições ainda mais complexas - use o notebook fornecido com esta postagem e altere o código ou tente suas novas habilidades em dados da vida real! Que a sorte esteja sempre a seu favor.



